摸球概率

同花顺

口袋里有100个球，编号从1到100。随机摸出1个，放到桌子上，再摸下一个，如果摸出的球的号码比桌子上的所有的球的号码都大就放到桌子上，否则扔掉，把100个球摸完，问最后桌子上有多少个球的概率最大？

昆仑苍狼

5 4 6 3 7 8 2 9

虎哥

5个, 概率基本是KK PREFLOP ALLIN AA的概率

                               
登錄/註冊後可看大圖

老陈

5, 21.08%4, 19.36%6, 17.88%3, 12.50%7, 11.71%8, 6.54%2, 5.09%9, 3.05%10, 1.21%1, 1.00%11, 0.42%12, 0.13%13, 0.03%14, 0.01%其它都特别小

昆仑苍狼

老陈 发表于 2015-9-27 01:405, 21.08%4, 19.36%6, 17.88%我就知道老陈会跳出来

                               
登錄/註冊後可看大圖

昆仑苍狼

期待值=1+1/100+1/99+1/98······1/3+1/2=5.19

Howard

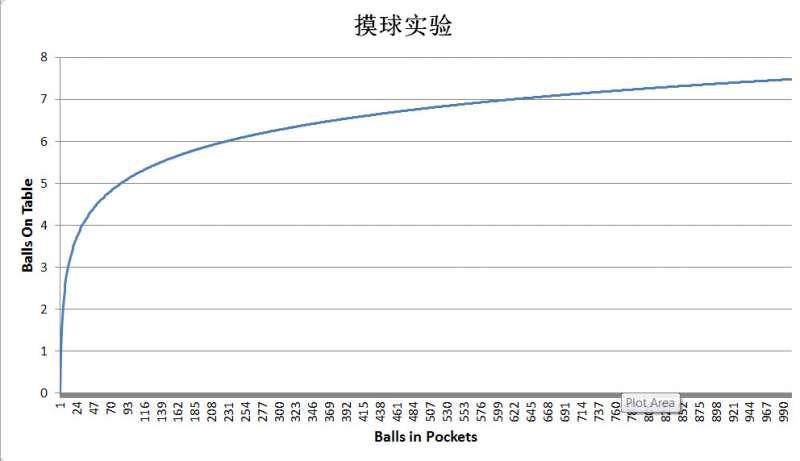
我对“桌上球最终长度的期望值”感兴趣。这个问题也适合倒叙推理，过程如下。如果桌上球最大号码是100，那么显然无论口袋里还剩下多少，摸球已经实际上结束。最终桌上球长度 = 现有桌上球长度 + 0；如果桌上球最大号码是99，那么100号球还在袋子里，当且仅当摸到它的时候，会上桌。最终桌上球长度 = 现有桌上球长度 + 1；为方便起见，以下用L0代表现有桌上球长度。L代表到结束为止期望再摸到的球数；（L0+L就是最终长度）N代表袋子里的起始球数（100）N0代表当前桌上球最大号码以上两步可以写为：N0=100，L=0；N0=99，L=1；如果N0=98，那么就有两种情况，第一种是先摸到99号，则L=1；第二种是先摸到100号，则L=0；这两种情况是对称的，概率各为1/2，再加上摸到的这一个也算1，所以最终球数期望值就是L = 1 + 1/2 * (1+0) = 1.5;如果N0=97，那么就有两种情况，第1种是先摸到100号，则L=0；第2种是先摸到99号，则L=1；第3种是先摸到98号，则L=1.5；这3种情况是对称的，概率各为1/3，再加上摸到的这一个也算1，所以最终球数期望值就是L = 1 + 1/3 * (1.5+1+0) = 1.833;.....不难总结出，N0 = t时的通项公式是：L = 1 + 1/(100-N0) * sum(N0从t到100的所有L)此公式用手计算虽然比较复杂，但是恰好是Spreadsheet的强项。用Excel计算，得出N0=0时，L = 5.1873775此处N0=0表示桌上一个球也没有，也就是还没有开始摸，所有此5.1873775就是桌上最终长度的期望值。继续计算可以得出，口袋里有1000个球时，桌上长度期望值为7.4855，只不过增长了2.3而已。下图列出了口袋球数与桌上长度期望值的关系：

091425xf2jgfgfqr2qt5kx.jpg

Howard

昆仑苍狼 发表于 2015-9-27 22:37期待值=1+1/100+1/99+1/98······1/3+1/2=5.19搞半天原来是Harmonic Series啊，怪不得看着眼熟

昆仑苍狼

Howard 发表于 2015-9-28 23:41搞半天原来是Harmonic Series啊，怪不得看着眼熟你的回复总是这么屌再请教 求摸出5个球的概率是多少的解析法

老陈

Howard 发表于 2015-9-28 09:14我对“桌上球最终长度的期望值”感兴趣。这个问题也适合倒叙推理，过程如下。要求最后桌上球的期望值，我想可以用如下方法计算：第1个球留在桌上的概率为1；第2个球号码比第1个大就留在桌上，小就不留，由于都是随机摸的，所以第2个球号码大的概率为1/2；当摸到第K个球，比较第K个球与桌上球号码最大的比较，实际上与前K-1个球相比较是不是最大是一样的，由于都是随机摸的，那么第K个球号码最大的概率为1/K；那么100个球摸完留在桌上的球数期望值如下：Σ1/K(K=1, 100)